A bar and hinge model formulation for structural analysis of curved-crease origami
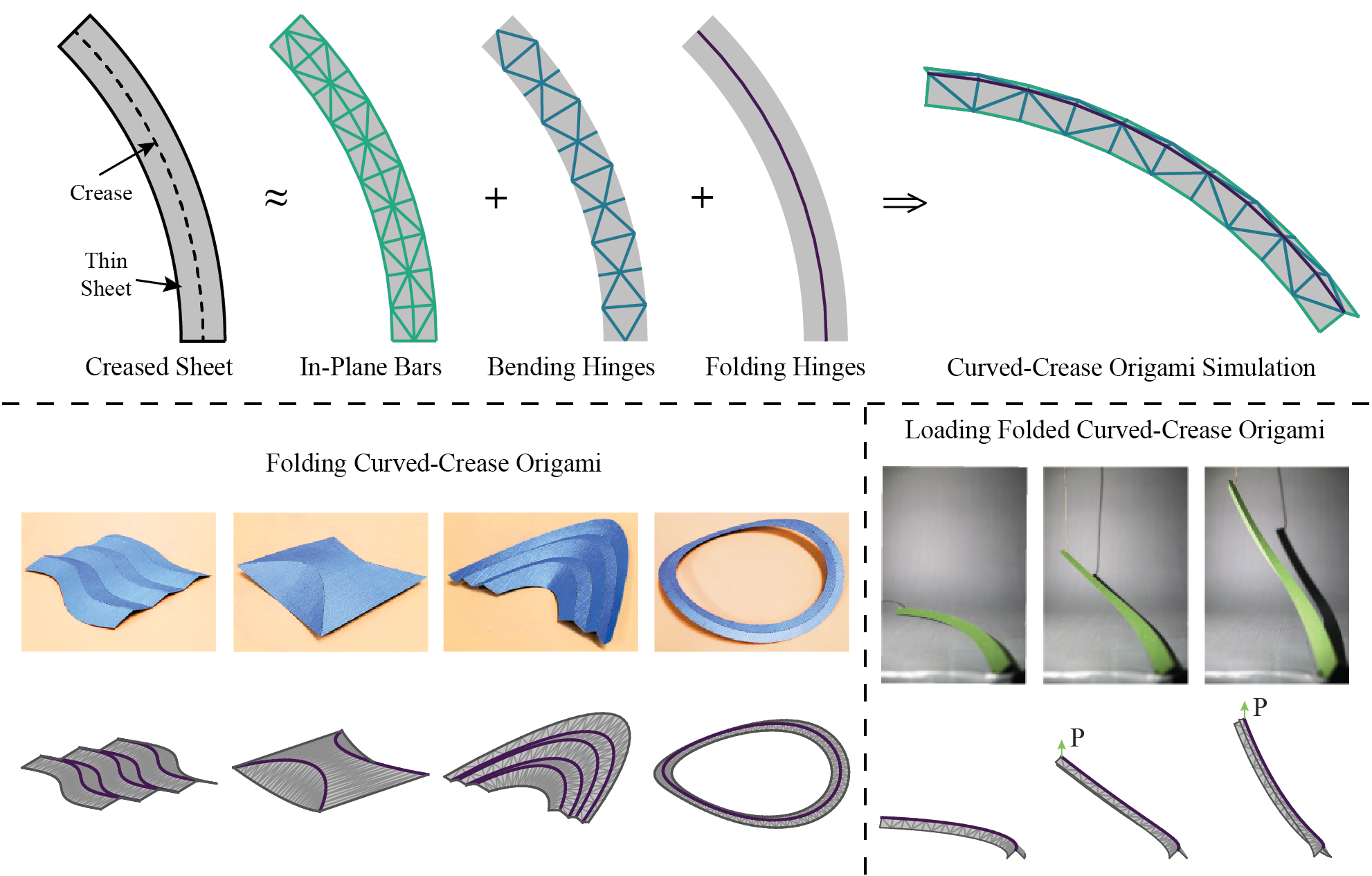
In this project, we develop and explore a method for simulating the structural properties of curved-crease origami through the use of a simplified numerical method called the bar and hinge model. We derive stiffness expressions for three deformation behaviors including stretching of the sheet, bending of the sheet, and folding along the creases. The stiffness expressions are based on system parameters that a user knows before analysis, such as the material properties of the sheet and the geometry of the flat fold pattern. We show that the model is capable of capturing folding behavior of curved-crease origami structures accurately by comparing deformed shapes to other theoretical and experimental approximations of the deformations. The model is used to study the structural behavior of a creased annulus sector and an origami fan. These studies demonstrate the versatile capability of the bar and hinge model for exploring the unique mechanical characteristics of curved-crease origami.
Curved creases redistribute global bending stiffness in corrugations: theory and experimentation
Corrugations offer a convenient way to make thin, lightweight sheets into stiff structures. However, traditional, straight-crease corrugations result in highly anisotropic stiffness which leads to undesirable flexibility in some directions of loading. In this project, we explore the bending stiffness of curved-crease corrugations – developable corrugations made by folding thin sheets about curves and without linerboard covers on the top or bottom. The curved-crease corrugations break symmetry in the pattern and can redistribute stiffness to resist bending deformations in multiple directions. We formulate a framework for predicting the bending stiffness of any general corrugation from its multiple geometric features at different scales. We use the framework to create two predictive methods that provide valuable insight to the global stiffness of corrugations without a detailed analysis. Results from these methods match well with experimental, three-point bending tests of five corrugation geometries made from polyester film. We found that corrugations with elliptical or parabolic curved-creases that intersect with one edge of the pattern are best at redistributing stiffness in multiple directions. While a straight-crease pattern has a stiffness of about 4 [N/mm] in one direction and about 0 [N/mm] in the other, a parabolic crease pattern has a stiffness of about 2.5 [N/mm] in both directions. These curved-crease corrugations can enable the self-assembly and fabrication of practical, stiff structures from simple, developable sheets. Link & PDF
Project Organization:
Principal Investigator: Prof. Evgueni T. Filipov,
Graduate Student: Steven Woodruff
Related Publication:
- Woodruff, S.R., and Filipov, E.T. (2020). A bar and hinge model formulation for structural analysis of curved-crease origami. (Submitted)
- Woodruff, S.R., and Filipov, E.T. (2020). Curved creases redistribute global bending stiffness in corrugations: theory and experimentation. Meccanica. (In Press) Link & PDF
- Woodruff, S.R., and Filipov, E.T. (2018). Structural Analysis of Curved Folded Deployables. ASCE Earth and Space, Cleveland, OH. Link
Acknowledgment:
The researchers of the project acknowledge support from ONR Grant N00014-18-1-2015. The summary and published papers reflect the views and position of the authors, and not necessarily those of the funding entities.
