Prof. E.T. Filipov’s previous research on folded structures focuses on mechanics of origami tubular structures.
Analytical models for thin-sheet structures
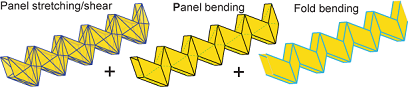
We have improved a model for the analysis of origami structures that consist of flat panels interconnected by a pattern of prescribed fold lines. This bar and hinge model, first introduced by Schenk and Guest (2011) can capture the fundamental behaviors of thin folded sheet structures. The model consists of three components: (1) elastic bar elements that simulate the stretching and shear stiffness thin panels; (2) rotational hinges that simulate folding of the panels; and (3) rotational hinges that simulate folding along the more flexible prescribed fold lines. We have made the model scalable, and have incorporated material characteristics such as the elastic modulus, Poisson’s ratio, and thickness of the thin sheet. Although this model is not as as accurate as a detailed finite element (FE) model it provides several useful advantages. The model is easy to implement, easy to use, it provides insightful results, and it is faster than FE analyses. The efficiency of the model makes it suitable for extensions to parametric studies, optimization or various specialized analyses.

Deployable coupled tube structures
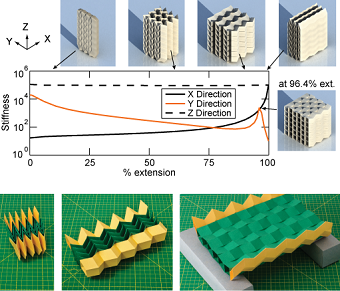
We have explored a variety of origami tube systems and assemblages. The basic type of tube is constructed by placing two symmetric Miura-ori sheets together (see Tachi 2009). The tube is rigid and flat foldable meaning it can fully unfold from a flattened state with deformations occurring only at the fold lines. We used eigenvalue and structural cantilever analysis to investigate and compare different geometries of tubes and coupled tube systems. The “zipper”-coupled tube system (shown on the left) yields an unusually large eigenvalue band-gap that represents a unique difference in stiffness between deformation modes. The structure has only one flexible mode through which it can deploy, yet it is significantly stiffer for all other bending and twisting type modes. The deployment motion is permitted by the flexible bending the thin sheet along the prescribed fold lines, however all other modes require the significantly stiffer stretching and shear of the thin sheet. The zipper-couped tubes have the advantages of deployable origami, but also the stiffening effect that is common in cellular/corrugated structures and materials.
Extensions from metamaterials to deployable architecture
Origami sheets and origami tubes can be coupled, combined, and arranged in a variety of methods to form new geometries and structures. We have shown different methods in which the zipper-coupled tubes can be assembled into cellular assemblages. By combining different types of coupled tubes together we can also enhance the structural characteristics of these systems. For example, the cubic cellular assemblage (shown top right) consists of zipper and aligned coupling, and has both space filling properties and the enhanced stiffness of the zipper tubes. This assemblage can have a variable asymmetrical stiffness depending on its configuration. Similarly, it is be possible to couple different geometries of tubes. To create a bridge type structure (shown bottom right), we use nearly square tubes to provide a smooth deck, and we use zippered zig-zag tubes to create a stiffer parapet. The deployable origami assemblages could lead to practical applications ranging in size from microscale metamaterials that harness the novel mechanical properties to large-scale deployable systems in engineering and architecture.
Publications related to this research:
- Filipov, E.T., Paulino G.H., and Tachi T. “Origami Tubes with Reconfigurable Polygonal Cross-Sections”. Proceedings of the Royal Society – A , Vol. 472, No. 2185, 20150607. See paper, details, and media coverage.
- Filipov, E.T., Tachi T., and Paulino G.H. (2015) “Origami Tubes Assembled Into Stiff, yet Reconfigurable Structures and Metamaterials,” Proceedings of the National Academy of Sciences USA , Vol. 112, No. 40, pp. 12321-12326. See paper, details, and media coverage.
- Filipov, E.T., Tachi, T., and Paulino, G.H. (2015). “Toward Optimization of Stiffness and Flexibility of Rigid, Flat-Foldable Origami Structures,” In Origami 6, Proc. of the 6th International Meeting on Origami Science, Mathematics, and Education (eds K Miura, T Kawasaki, T Tachi, R Uehara, RJ Lang, P Wang-Iverson), pp. 409–419. Providence, RI: American Mathematical Society.
Press coverage:
Highlighted in PNAS commentary by Reis et al. 2015. Reported by: WXYZ TV – ABC News, Civil + Structural Engineer, Discovery News, Motherboard, City Lab, Fast Company, Gizmag, Phys.org, Science Daily, Space Daily, Gizmodo, Sydney Morning Herald, also more on zipper tubes and more on polygonal tubes.